Conversion lumen, candela et stéradian

Lumen, candela ou stéradian? La lumière concentrée d’une lampe torche se décrit en candelas alors qu’une puissante ampoule fournit un flux élevé en lumens dans toutes les directions. Il s’agit de comprendre la notion de lumen (lumière totale émise), de stéradian (la portion d’espace vers où la lumière est émise) et de candela (l’intensité lumineuse dans une direction donnée).

Le flux lumineux d’une source se mesure en lumens mais si cette source éclaire dans une direction précise, il est utile de parler de candela. Pourquoi ? L’angle solide est une notion clé pour comprendre cette conversion. On l’explique ici de façon simple et abordable.

Intensités lumineuses variables

Ici, lorsqu’on concentre plus ou moins le faisceau lumineux d’une lampe torche, la lumière totale émise est toujours la même (la quantité de lumens ne change pas), mais le faisceau concentré éclaire une plus petite portion d’espace (angle solide en stéradian plus faible) et du coup, l’intensité lumineuse est plus forte (davantage de candelas).

Conversion lumen, candela et stéradian : définition

La relation lumen (lm), candela (cd) et stéradian (sr) s’écrit :

1 candela = 1 lumen / stéradian

ou :

1 cd = 1 lm/sr

Ci dessous, quelques définitions (utiles) sont précisées et commentées : lumen, radian, stéradian et enfin… candela !

Le lumen : une unité de puissance comme le Watt

Le lumen, de symbole lm, est une unité de puissance lumineuse comme le watt (W). Il décrit la quantité totale de lumière émise par une source lumineuse (ampoule, LED, etc). Comme la conversion minute-seconde (mesure du temps) ou dollar-euro, on a la conversion :

1 W = 683 lm (à 555 nm)

Cette conversion n’est valable que pour la longueur d’onde 555 nm. Pour une couleur où la sensibilité de l’oeil est de 10 % du maximum (rouge ou violet par exemple), 1 watt correspond à 683 lm x 10% = 68,3 lm. Une rayonnement emis à 350 nm (UV) ou 900 nm (infrarouge) n’est pas perçu par l’œil et correspond donc à 0 lumen.

Sensibilité de l’œil humain : l’œil voit des lumens, pas des Watts

Le lumen tient compte de la sensibilité de l’œil humain.

Le stéradian : unité d’angle solide

Qu’est-ce que le stéradian ?

Première intuition sur l’angle solide

L’angle solide décrit la portion d’espace embrassée par le regard d’un observateur. Un petit objet vu de près peut paraître occuper le champ visuel de la même façon qu’un gros objet éloigné : ils ont la même taille apparente. L’angle solide qu’ils occupent est identique.

Angle solide identique pour S1, S2 et S3

Le plus grand angle solide possible correspond à tout l’espace (regarder dans n’importe quelle direction), comme un angle de 360° qui correspond à toutes les directions du plan.

Définition de l’angle (en 2D)

La définition de l’angle (en radian) permet d’introduire la définition d’angle solide.

La longueur L d’un arc de cercle intercepté par 2 droites est proportionnelle au rayon du cercle. On peut écrire :

L = αR

Ce coefficient de proportionnalité α, c’est l’angle !

Définition de l’angle en radian (rad)

Si l’arc mesure un tour complet, on a :

longueur de l’arc = circonférence totale

αR = 2πR

α = 2π

Un tour complet correspond à 2π radians (=360 degrés).

Note : le radian est le rapport de 2 longueurs et n’a donc pas d’unité.

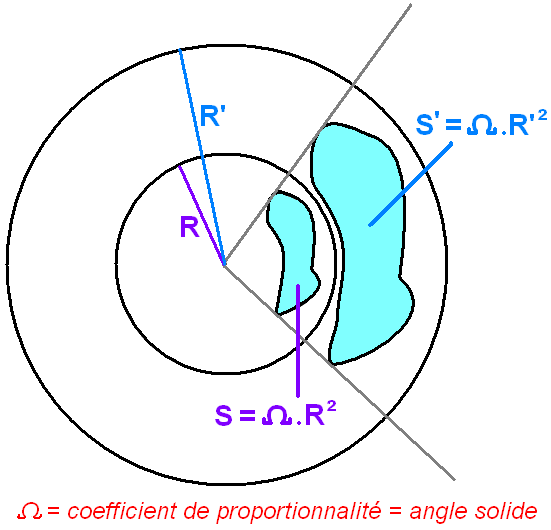
Définition de l’angle solide (en 3D)

On constate que la surface S d’une portion de sphère est proportionnelle au carré du rayon de la sphère. On peut écrire :

S = ΩR²

Ce coefficient de proportionnalité Ω, c’est l’angle solide !

Définition de l’angle solide en stéradian (sr)

Si la surface S correspond à toute la sphère, on a :

surface = surface totale de la sphère

ΩR² = 4πR²

Ω = 4π

Toute la surface de la sphère correspond à 4π stéradians.

Note : le stéradian est le rapport de 2 surfaces et n’a donc pas d’unité.

Pour un même angle d’ouverture, l’intensité lumineuse est proportionnelle au flux émis par l’ampoule.

Le candela : unité d’intensité lumineuse

La définition du candela est : 1 candela = 1 lumen / stéradian

Angle et angle solide

Lorsque l’angle d’ouverture α d’un cône est petit, l’angle solide varie environ avec le carré de cet angle.

Pour des faisceaux concentrés, l’intensité lumineuse décroît approximativement avec le carré de l’angle d’ouverture du faisceau.

Exemple :

10° d’angle : 400 cd

20° d’angle : 100 cd environ

Pour une ampoule sans réflecteur (qui émet autant de lumière dans toutes les directions), on a le rapport :

Intensité lumineuse (cd) = Flux (lm) / (4π)

Exemple : ampoule halogène 12 V, 50 W, 900 lm

Flux : 900 lm

Intensité lumineuse : 900 / (4 x 3,14) = 72 cd environ

Attention : la notion d’intensité lumineuse ne concerne que la source lumineuse, jamais l’objet éclairé. Pour l’objet éclairé, on parle d’éclairement. L’éclairement se mesure en lux.

Applications : lampes halogène à réflecteur et LED

Lorsque la lumière est dirigée dans une direction précise, les fabricants parlent de candela (cd) pour les lampes halogène ou millicandela (mcd) pour les LED. A puissance constante (lumens émis), plus une lampe ou une LED émet un faisceau concentré, plus l’intensité lumineuse est élevée. Pour une même source lumineuse (filament), le réflecteur joue un rôle crucial dans l’intensité lumineuse finale.

Lampes halogène

La forme du réflecteur d’une lampe halogène détermine l’angle d’ouverture et ainsi l’intensité lumineuse de la lampe (exemple ci dessous) :

Faisceau concentré : beaucoup de candelas

Intensité lumineuse en fonction de l’angle d’ouverture

Chez un fabricant de lampes halogène de différentes puissances et différents réflecteurs, on peut trouver :

Intensité lumineuse fonction de l’angle d’ouverture et de la puissance

On remarque l’intensité lumineuse décroit avec l’angle d’ouverture et augmente avec la puissance de l’ampoule. En revanche, le flux lumineux (lumens) ne dépend que de la puissance de l’ampoule. Peu importe comment toute cette lumière est réfléchie !

LED : millicandelas et lumens

Pour les LED, le même phénomène existe en fonction de la forme du boitier plastique transparent où loge la puce émettrice de lumière.

La concurrence pousse les fabricants de LED à offrir des luminosités (comprendre : intensité lumineuse)toujours plus grandes ! Pour une LED 5 mm de forte puissance, la luminosité peut atteindre 80 000 mcd (c’est-à-dire 80 candelas).

Note : 80 000 mcd = 80 kmcd = 80 cd (kilo-milli, ça se compense…)

Puces identiques intégrées dans des boîtiers différents

Avec un angle de 40°, la lumière est plus concentrée et l’intensité lumineuse est plus élevée mais le flux lumineux total est identique. Le fabricant ne précise pas combien de lumens génèrent ces LED.

D’autres fabricants de LED de puissance indiquent, au contraire le flux lumineux émis. C’est pertinent (et marketing !) pour de grands angles d’ouverture (140° typiques). En effet, le but est plutôt d’éclairer une large zone, comme le fait une ampoule. Le flux lumineux intéressera l’utilisateur pour pouvoir comparer à une ampoule. De plus, l’intensité lumineuse serait assez faible puisque l’angle est très grand.

Exemple :

LED blanche 20 W pour éclairage

• Flux : 1600 lumens (équivalent à 125 W d’ampoule à incandescence !)
• Angle : 140°
• Intensité lumineuse : 300 cd environ

L’ajout un réflecteur parabolique à cette LED pourra faire augmenter son intensité lumineuse énormément, mais pas le flux lumineux !

Conclusion : lumen et candela

Lumens et candelas mesurent des quantités de lumière mais différemment. Le lumen mesure un flux total émis, toutes directions confondues. En revanche, le candela mesure l’intensité lumineuse dans un angle solide donné. Plus on concentre un même faisceau de lumière, plus l’intensité lumineuse augmente alors que le flux lumineux total ne varie pas.