
La fonction de Dirac, qu’on doit appeler distribution de Dirac, est nulle partout, sauf en un seul point où elle prend une valeur infinie.
Sommaire
La distribution de Dirac 𝛿(𝑡)
la fonction delta de Dirac, notée 𝛿(𝑡), est une entité singulière et fascinante en mathématiques et en physique. Contrairement aux fonctions classiques, elle appartient au cadre des distributions (ce n’est pas une fonction parce qu’une fonction ne peut pas prendre une valeur infinie). Elle est définie comme étant nulle partout sauf en t = 0, où elle atteint une valeur infinie, de telle sorte que son intégrale sur l’ensemble du temps (de -∞ à +∞) vaut exactement 1 :
et son intégrale :
Cette propriété étonnante soulève une question : comment une telle impulsion peut-elle contenir toutes les fréquences ?
Temps et fréquence
Dans l’étude des signaux et des systèmes, deux représentations coexistent :
- Le domaine temporel, qui décrit l’évolution d’un signal au fil du temps.
- Le domaine fréquentiel, qui indique la répartition du signal selon les différentes bandes de fréquence.
Pour passer d’un domaine à l’autre, on utilise la transformée de Fourier.
La transformée de Fourier
Vous trouverez partout la formule de la transformée de Fourier sur le net, mais comment en développer une intuition ? La transformée de Fourier d’une fonction 𝑓(𝑡) est une fonction complexe 𝐹(𝜔) qui révèle son spectre fréquentiel. On visualise le spectre fréquentiel d’un signal musical qu’on peut décomposer des plus basses fréquences (graves) aux plus hautes fréquences (aigus). Dans le domaine de la lumière, c’est comme un prisme qui décompose les différentes couleurs de l’arc-en-ciel. La lumière blanche contient toutes les couleurs, c’est-à-dire toutes les fréquences.
Le delta de Dirac en fréquence
Appliquons cette transformée de Fourier à la fonction delta de Dirac 𝛿(𝑡). Le résultat, la transformée de Fourier de 𝛿(𝑡) est une constante égale à 1. Cela signifie que la fonction delta de Dirac contient toutes les fréquences avec la même intensité. Il y autant de toutes les fréquences.
Pour les amatrices et amateurs de bruit, le bruit dit blanc contient lui aussi autant de toutes les fréquences, mais se présente comme uniforme au cours du temps.
Intuition et analogies pour la fonction delta de Dirac 𝛿(𝑡)
Pour mieux saisir cette idée, imaginons une analogie musicale :
Frapper une note de piano, par exemple un la 440 Hz. L’auditeur percevra un la 440 Hz. Imaginez que la durée de la note soit de plus en plus courte. L’auditeur percevra de moins en moins bien la hauteur de la note. Frapper une note parfaitement instantanée sur un piano idéal produirait un son qui résonne simultanément à toutes les fréquences. L’auditeur n’aurait pas le temps d’identifier quoi que ce soit. On entendrait un gros « tac », très fort et très court. De même, la fonction delta de Dirac représente une impulsion infiniment brève qui excite l’ensemble du spectre fréquentiel. Un « tac » infiniment fort, mais infiniment bref.
Une note de piano infiniment courte : on ne peut plus reconnaître la hauteur de la note. Il y a toutes les fréquences…
On peut aussi l’interpréter en termes de bande passante : un signal parfaitement localisé dans le temps possède une bande passante infinie. Comme une goutte colorée qui se diffuse uniformément dans l’eau, la fonction delta de Dirac 𝛿(𝑡) s’étend sur toutes les fréquences.
Conclusion
La fonction delta de Dirac illustre une dualité intéressante : concentrée à l’extrême dans le temps, elle s’étend infiniment dans le domaine fréquentiel. Cette propriété en fait un élément de base de l’analyse de Fourier et du traitement du signal dans le domaine électronique et mathématique.

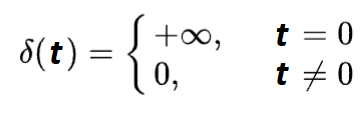
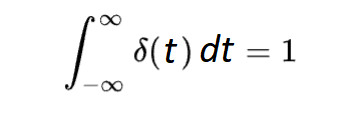

Laisser un commentaire